密码学实验

密码学的实验报告，密码学真的难，DES完全是只知道思路但是写不出代码，最后到github参考了别人的代码才勉强修改完成，哈希稍微好些，可以选择，选了SHA-256以后简单的做了一个不加盐的函数，但是仍旧不是自己完全写出来的成果，ORZ…
过程很辛苦，查了很多资料，看了很多别人的实现方法，还是记录一下。

古典密码

凯撒密码

在密码学中，恺撒密码（英语：Caesar cipher），或称恺撒加密、恺撒变换、变换加密，是一种最简单且最广为人知的加密技术。它是一种替换加密的技术，明文中的所有字母都在字母表上向后（或向前）按照一个固定数目进行偏移后被替换成密文。例如，当偏移量是3的时候，所有的字母A将被替换成D，B变成E，以此类推。这个加密方法是以罗马共和时期恺撒的名字命名的，当年恺撒曾用此方法与其将军们进行联系。

凯撒安全性分析

由于英文只有26个字母，而且可以通过求余降幂，规模最大为26。完全可以暴力攻击。

加密

#include<iostream>
#include<string.h>
#include<string>
using namespace std;
char cry[1000010];
//char enc[1000010];
int main(){
  int t,k;
  int i;
  scanf("%d",&t);
  while(t–){
     memset(cry,'\0',sizeof(cry));
     //memset(enc,'\0',sizeof(enc));
     scanf("%s",cry);
     scanf("%d",&k);
     //printf("%d",k);
     //for(i=0;cry[i]!='\0';i++);
     k=k%26;
     for(int i=0;cry[i]!='\0';i++){
         if(cry[i]<'A'||cry[i]>'z'||(cry[i]>'Z'&&cry[i]<'a')){
            cry[i]=cry[i];
         }
         else
         if((cry[i]-k>'Z'&&(cry[i]>='A'&&cry[i]<='Z'))||(cry[i]-k>'z'&&(cry[i]>='a'&&cry[i]<='z'))){
            cry[i]=char(cry[i]+k-26);
         }
         else
         if((cry[i]-k<'A'&&(cry[i]>='A'&&cry[i]<='Z'))||(cry[i]-k<'a'&&(cry[i]>='a'&&cry[i]<='z'))){
            cry[i]=char(cry[i]+26-k);
         }
         else{
            cry[i]=char(cry[i]-k);
         }
     }
     printf("%s\n",cry);
  }
  //cout<<cry;
}

破解

#include<iostream>
#include<string.h>
#include<string>
//unknow K7
using namespace std;
char cip[1000010];
char tr[1000010];
int main(){
  memset(cip,'\0',sizeof(cip));
  scanf("%s",cip);
  for(int k=25;k>=0;k–){
     printf("key=%d\n",26-k);
     for(int i=0;cip[i]!='\0';i++){
         if(cip[i]<'A'||cip[i]>'z'||(cip[i]>'Z&&cip[i]<'a')){'
            tr[i]=cip[i];
         }
         else
         if((cip[i]-k>'Z'&&(cip[i]>='A'&&cip[i]<='Z'))||(cip[i]-k>'z'&&(cip[i]>='a'&&cip[i]<='z'))){
            tr[i]=char(cip[i]+k-26);
         }
         else
         if((cip[i]-k<'A'&&(cip[i]>='A'&&cip[i]<='Z'))||(cip[i]-k<'a'&&(cip[i]>='a'&&cip[i]<='z'))){
            tr[i]=char(cip[i]+26-k);
         }
         else{
            tr[i]=char(cip[i]-k);
         }
     }
     printf("%s\n",tr);
  }
}

程序运行截图

维吉尼亚密码

维吉尼亚密码（又译维热纳尔密码）是使用一系列凯撒密码组成密码字母表的加密算法，属于多表密码的一种简单形式。
维吉尼亚密码曾多次被发明。该方法最早记录在吉奥万·巴蒂斯塔·贝拉索（ Giovan Battista Bellaso）于1553年所著的书《吉奥万·巴蒂斯塔·贝拉索先生的密码》（意大利语：La cifra del. Sig.Giovan Battista Bellaso）中。然而，后来在19世纪时被误传为是法国外交官布莱斯·德·维吉尼亚（Blaise De Vigenère）所创造，因此现在被称为“维吉尼亚密码”。

仿射密码的安全性分析

弗里德曼试验由威廉·F·弗里德曼（William F. Friedman）于1920年代发明。他使用了重合指数（index of coincidence）来描述密文字母频率的不匀性，从而破译密码。

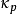
指目标语言中两个任意字母相同的概率（英文中为0.067），

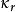
指字母表中这种情况出现的概率（英文中为1/26=0.0385），从而密钥长度可以估计为：

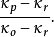
其中，观察概率为

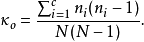
其中，c是指字母表的长度（英文为26），N指文本的长度，n1到n是指密文的字母频率，为整数。
此方法只是一种估计，会随着文本长度的增加而更为精确。在实践中，会尝试接近此估计的多个密钥长度。一种更好的方法是将密文写成矩阵形式，其中列数与假定的密钥长度一致，将每一列的重合指数单独计算，并求得平均重合指数。对于所有可能的密钥长度，平均重合指数最高的最有可能是真正的密钥长度。这样的试验可以作为卡西斯基试验的补充。

频率分析

一旦能够确定密钥的长度，密文就能重新写成多列，列数与密钥长度对应。这样每一列其实就是一个凯撒密码，而此密码的密钥（偏移量）则对应于维吉尼亚密码密钥的相应字母。与破译凯撒密码类似的方法，就能将密文破译。
柯克霍夫方法作为卡西斯基试验的改进，由奥古斯特·柯克霍夫（Auguste Kerckhoffs）提出。它将每一列的字母频率与转换后的明文频率相对应而得出每一列的密钥字母。一旦密钥中每一个字母都能确定，就能很简单地破译密文，从而得到明文。如果维吉尼亚字母表表格本身是杂乱而非按通常字母表顺序的话，那柯克霍夫方法就会无效，但卡西斯基试验和重复指数对于决定密钥长度仍旧是有效的。

加密

#include<iostream>
#include<string.h>
#include<string>
using namespace std;
char k[105];
char cyp[1010];
int main(){
         //scanf("%s",&k);
         //getline(cin,1010);
         scanf("%s%[^\n]",&k,&cyp);
         int clen,klen;
         /**for(clen=0;cyp[clen]!=’\0’;clen++){
           if(cyp[clen]>’Z’){
              cyp[clen]=char(cyp[clen]-(‘a’-‘A’));
           }
         }**/
         for(klen=0;k[klen]!=’\0’;klen++){
           if(k[klen]>’Z’){
              k[klen]=char(k[klen]-(‘a’-‘A’));
           }
         }
         //printf("%s",k);
         int j=0;
         for(int i=0;cyp[i]!=’\0’;i++){
           if(cyp[i]>=’A’&&cyp[i]<=’Z’){
              if(cyp[i]+(k[j%klen]-‘A’)>’Z’){
                  cyp[i]=char(cyp[i]-(26-(k[j%klen]-‘A’)));
              }
              else{
                  cyp[i]=char(cyp[i]+(k[j%klen]-‘A’));
              }
              j++;
           }
           else if(cyp[i]==’ ‘||cyp[i]==’.’||cyp[i]==’,’||cyp[i]==’'‘){
              //cyp[i]=’‘;
           }
           else{
              if(cyp[i]+(k[j%klen]-‘A’)>’z’){
                  cyp[i]=char(cyp[i]-(26-(k[j%klen]-‘A’)));
              }
              else{
                  cyp[i]=char(cyp[i]+(k[j%klen]-‘A’));
              }
              j++;
           }
         }
         printf("%s\n",cyp);
}

破解

from string import ascii_lowercase as lowercase

#需要大量的明文支撑
def VigenereDecrypto(output, key):
    ptLen = len(output)
    keyLen = len(key)
    quotient = ptLen // keyLen
    remainder = ptLen % keyLen
    inp = ""
    for i in range(0, quotient):
        for j in range(0, keyLen):
            c = int((ord(output[i * keyLen + j]) - ord('a') - (ord(key[j]) - ord('a'))) % 26 + ord('a'))
            inp += chr(c)
    for i in range(0, remainder):
        c = int((ord(output[quotient * keyLen + i]) - ord('a') - (ord(key[i]) - ord('a'))) % 26 + ord('a'))
        # global input
        inp += chr(c)
    return inp
#纯文本
def get_trim_text(text):
    text = text.lower()
    trim_text = ''
    for l in text:
        if lowercase.find(l) >= 0:
            trim_text += l
    return trim_text

# 计算IC
def get_coincidence_index(text):
    text = get_trim_text(text)
    length = len(text)
    letter_stats = []
    for l in lowercase:
        lt = {}
        count = text.count(l)#统计
        lt[l] = count
        letter_stats.append(lt)

    index = 0
    for d in letter_stats:
        v = list(d.values())[0]
        index += (float(v) / length) ** 2

    return index


# 与0.67比较
def get_var(data, mean=0.065):
    if not data:
        return 0
    var_sum = 0
    for d in data:
        var_sum += (d - mean) ** 2

    return float(var_sum) / len(data)

# 爆破密钥长度
def get_key_length(text):
    # assume text length less than 26
    text = get_trim_text(text)
    group = []
    for n in range(1, len(text) + 1):
        group_str = ['' for i in range(n)]
        for i in range(len(text)):
            l = text[i]
            for j in range(n):
                if i % n == j:
                    group_str[j] += l
        group.append(group_str)
    var_list = []
    length = 1
    for tex in group:
        data = []
        for t in tex:
            index = get_coincidence_index(t)
            data.append(index)
        var_list.append([length, get_var(data)])
        length += 1
    var_list = sorted(var_list, key=lambda x: x[1])#
    return [v[0] for v in var_list[:int(n / 2) + 1]]  #
# 统计字频，分组
def countList(lis):
    li = []
    alphabet = [chr(i) for i in range(97, 123)]
    for c in alphabet:
        count = 0
        for ch in lis:
            if ch == c:
                count += 1
        li.append(float(count) / len(lis))
    return li
# 根据密钥长度分组密文
def textToList(text, length):
    text = get_trim_text(text)
    textMatrix = []
    row = []
    index = 0
    for ch in text:
        row.append(ch)
        index += 1
        if index % length == 0:
            textMatrix.append(row)
            row = []
    textMatrix.append(row)
    return textMatrix


# 获取密钥
def getKey(text, length):
    text = get_trim_text(text)
    key = []  # 存密钥
    alphaRate = [0.08167, 0.01492, 0.02782, 0.04253, 0.12705, 0.02228, 0.02015, 0.06094,
                 0.06996, 0.00153, 0.00772, 0.04025, 0.02406, 0.06749, 0.07507, 0.01929,
                 0.0009, 0.05987, 0.06327, 0.09056, 0.02758, 0.00978, 0.02360, 0.0015, 0.01974, 0.00074]#��Ȼ���ɣ�������
    matrix = textToList(text, length)
    for i in range(length):
        w = [row[i] for row in matrix if len(row) > i]  # 获取密文
        li = countList(w)
        powLi = []  # 算乘积
        for j in range(26):
            Sum = 0.0
            for k in range(26):
                Sum += alphaRate[k] * li[k]
            powLi.append(Sum)
            li = li[1:] + li[:1]  # 循环移位
        Abs = 100
        ch = ''
        for j in range(len(powLi)):
            if abs(powLi[j] - 0.065546) < Abs:  # 找出最接近IC的项
                Abs = abs(powLi[j] - 0.065546)  # 保存最接近的距离，作为下次比较的基准
                ch = chr(j + 97)
        key.append(ch)
    return key
key_lengths = []
c = input("输入密文：")
key_lengths = get_key_length(c)
print(key_lengths)
for i in range(len(key_lengths)):
    key = getKey(c,key_lengths[i])
    print("明文%s, 密钥长度是 %d, 密钥是 %s" \
          % (VigenereDecrypto (c , key), key_lengths[i], key))

程序运行截图

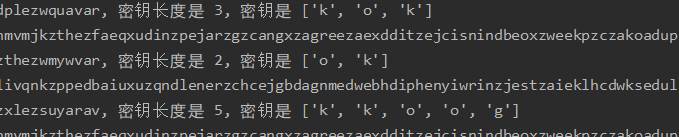
分组密码

DES过程分析

所需参数

key:8个字节共64位密钥

data：8个字节共64位需要被加密的明文

初始置换

DES算法使用64位的密钥key将64位的明文输入块变为64位的密文输出块，并把输出块分为L0、R0两部分，每部分均为32位。初始置换规则如下：

1.  58,50,42,34,26,18,10,2,  

2.  60,52,44,36,28,20,12,4,  

3.  62,54,46,38,30,22,14,6,  

4.  64,56,48,40,32,24,16,8,  

5.  57,49,41,33,25,17, 9,1,  

6.  59,51,43,35,27,19,11,3,  

7.  61,53,45,37,29,21,13,5,  

8.  63,55,47,39,31,23,15,7,  

加密-迭代处理函数（F函数）

经过初始置换之后，进行16轮完全相同的运算，在运算过程中数据与密钥结合。

函数F的输出经过一个异或运算，和左半部分结合形成新的右半部分，原来的右半部分成为新的左半部分。

F函数：是由四步运算构成：密钥置换；拓展置换；S盒代替；P置换；

密钥置换—子密钥生成：DES算法由64位密钥产生16轮的48位子密钥。在每一轮的迭代过程中，使用不同的子密钥。

1. 把密钥的奇偶校验位忽略不参与计算，即每个字符的第8位，将6位密钥降为56位，让后根据选择置换PC-1将56位分成2块C0和D0各28位。

2. 将C0和D0进行循环左移变化（美伦循环作业的位数由轮数决定），变换后产生C1和D1，然后C1和D1合并，并通过选择置换pc-2生成子密钥k1（48位）

3. C1和D1再次经过循环左移变换，生成C2和D2，然后合并C2，D2，通过选择置换pc—2生成密钥K2（48位）

4. 以此类推，得到K16。最后一轮的左右两部分不交换，而是直接合并在一起R16L16，作为逆置换的输入块。

密钥置换选择1  PC—1

64位秘钥降至56位秘钥不是说将每个字节的第八位删除，而是通过缩小选择换位表1（置换选择表1）的变换变成56位。

1.  57,49,41,33,25,17,9,1,  

2.  58,50,42,34,26,18,10,2,  

3.  59,51,43,35,27,19,11,3,  

4.  60,52,44,36,63,55,47,39,  

5.  31,23,15,7,62,54,46,38,  

6.  30,22,14,6,61,53,45,37,  

7.  29,21,13,5,28,20,12,4  

                  

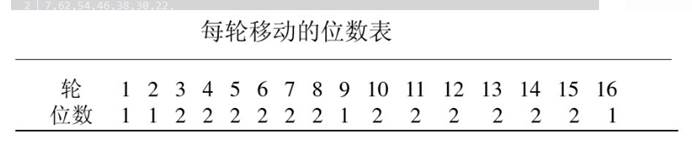再将56位秘钥分成C0和D0, 根据轮数，将Cn和Dn分别循环左移1位或2位.

扩展置换E(E位选择表)

通过扩展置换E，数据的右半部分Rn从32位扩展到48位。扩展置换改变了位的次序，重复了某些位。扩展置换的目的：a、产生与秘钥相同长度的数据以进行异或运算，R0是32位，子秘钥是48位，所以R0要先进行扩展置换之后与子秘钥进行异或运算；b、提供更长的结果，使得在替代运算时能够进行压缩。扩展置换E规则如下：

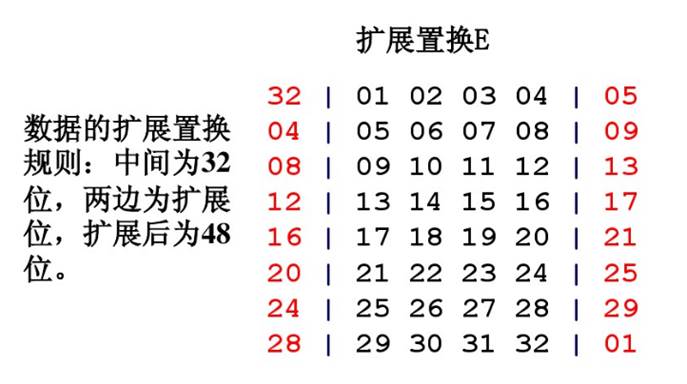
S-盒代替(功能表S盒)

Rn扩展置换之后与子秘钥Kn异或以后的结果作为输入块进行S盒代替运算功能是把48位数据变为32位数据代替运算由8个不同的代替盒(S盒)完成。每个S-盒有6位输入，4位输出。所以48位的输入块被分成8个6位的分组，每一个分组对应一个S-盒代替操作。经过S-盒代替，形成8个4位分组结果。注意：每一个S-盒的输入数据是6位，输出数据是4位，但是每个S-盒自身是64位！！每个S-和是4行16列的格式，因为二进制4位是0~15。
8个S-盒的值如下：

1.     // S1  

2.     14, 4,  13,     1,  2, 15, 11,  8,  3, 10,  6, 12,  5,  9,  0,  7,  

3.     0, 15,  7,  4, 14,  2, 13,  1, 10,  6, 12, 11,  9,  5,  3,  8,  

4.     4,  1, 14,  8, 13,  6,  2, 11, 15, 12,  9,  7,  3, 10,  5,  0,  

5.     15, 12,  8,  2,  4,  9,  1,  7,  5, 11,  3, 14, 10,  0,  6, 13,  

6.     // S2  

7.     15,  1,  8, 14,  6, 11,  3,  4,  9,  7,  2, 13, 12,  0,  5, 10,  

8.     3, 13,  4,  7, 15,  2,  8, 14, 12,  0,  1, 10,  6,  9, 11,  5,  

9.     0, 14,  7, 11, 10,  4, 13,  1,  5,  8, 12,  6,  9,  3,  2, 15,  

10.    13,  8, 10,  1,  3, 15,  4,  2, 11,  6,  7, 12,  0,  5, 14,  9,  

11.    // S3  

12.    10,  0,  9, 14,  6,  3, 15,  5,  1, 13, 12,  7, 11,  4,  2,  8,  

13.    13,  7,  0,  9,  3,  4,  6, 10,  2,  8,  5, 14, 12, 11, 15,  1,  

14.    13,  6,  4,  9,  8, 15,  3,  0, 11,  1,  2, 12,  5, 10, 14,  7,  

15.    1, 10, 13,  0,  6,  9,  8,  7,  4, 15, 14,  3, 11,  5,  2, 12,  

16.    // S4  

17.    7, 13, 14,  3,  0,  6,  9, 10,  1,  2,  8,  5, 11, 12,  4, 15,  

18.    13,  8, 11,  5,  6, 15,  0,  3,  4,  7,  2, 12,  1, 10, 14,  9,  

19.    10,  6,  9,  0, 12, 11,  7, 13, 15,  1,  3, 14,  5,  2,  8,  4,  

20.    3, 15,  0,  6, 10,  1, 13,  8,  9,  4,  5, 11, 12,  7,  2, 14,  

21.    // S5  

22.    2, 12,  4,  1,  7, 10, 11,  6,  8,  5,  3, 15, 13,  0, 14,  9,  

23.    14, 11,  2, 12,  4,  7, 13,  1,  5,  0, 15, 10,  3,  9,  8,  6,  

24.    4,  2,  1, 11, 10, 13,  7,  8, 15,  9, 12,  5,  6,  3,  0, 14,  

25.    11,  8, 12,  7,  1, 14,  2, 13,  6, 15,  0,  9, 10,  4,  5,  3,  

26.    // S6  

27.    12,  1, 10, 15,  9,  2,  6,  8,  0, 13,  3,  4, 14,  7,  5, 11,  

28.    10, 15,  4,  2,  7, 12,  9,  5,  6,  1, 13, 14,  0, 11,  3,  8,  

29.    9, 14, 15,  5,  2,  8, 12,  3,  7,  0,  4, 10,  1, 13, 11,  6,  

30.    4,  3,  2, 12,  9,  5, 15, 10, 11, 14,  1,  7,  6,  0,  8, 13,  

31.    // S7  

32.    4, 11,  2, 14, 15,  0,  8, 13,  3, 12,  9,  7,  5, 10,  6,  1,  

33.    13,  0, 11,  7,  4,  9,  1, 10, 14,  3,  5, 12,  2, 15,  8,  6,  

34.    1,  4, 11, 13, 12,  3,  7, 14, 10, 15,  6,  8,  0,  5,  9,  2,  

35.    6, 11, 13,  8,  1,  4, 10,  7,  9,  5,  0, 15, 14,  2,  3, 12,  

36.    // S8  

37.    13,  2,  8,  4,  6, 15, 11,  1, 10,  9,  3, 14,  5,  0, 12,  7,  

38.    1, 15, 13,  8, 10,  3,  7,  4, 12,  5,  6, 11,  0, 14,  9,  2,  

39.    7, 11,  4,  1,  9, 12, 14,  2,  0,  6, 10, 13, 15,  3,  5,  8,  

40.    2,  1, 14,  7,  4, 10,  8, 13, 15, 12,  9,  0,  3,  5,  6, 11  

P盒置换：

S-盒代替运算，每一盒得到4位，8盒共得到32位输出。这32位输出作为P盒置换的输入块。P盒置换将每一位输入位映射到输出位。任何一位都不能被映射两次，也不能被略去。经过P-盒置换的结果与最初64位分组的左半部分异或，然后左右两部分交换，开始下一轮迭代。P-盒置换表(表示数据的位置)共32位

1.  16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,  

2.  2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25,  

逆置换

将初始置换进行16次的迭代，即进行16层的加密变换，这个运算过程我们暂时称为函数f。得到L16和R16，将此作为输入块，进行逆置换得到最终的密文输出块。逆置换是初始置换的逆运算。从初始置换规则中可以看到，原始数据的第1位置换到了第40位，第2位置换到了第8位。则逆置换就是将第40位置换到第1位，第8位置换到第2位。以此类推，逆置换规则如下

1.  40,8,48,16,56,24,64,32,39,7,47,15,55,23,63,31,  

2.  38,6,46,14,54,22,62,30,37,5,45,13,53,21,61,29,  

3.  36,4,44,12,52,20,60,28,35,3,43,11,51,19,59,27,  

4.  34,2,42,10,50,18,58 26,33,1,41, 9,49,17,57,25,  

解密

加密和解密可以使用相同的算法。加密和解密唯一不同的是秘钥的次序是相反的。就是说如果每一轮的加密秘钥分别是K1、K2、K3…K16，那么解密秘钥就是K16、K15、K14…K1。为每一轮产生秘钥的算法也是循环的。加密是秘钥循环左移，解密是秘钥循环右移。解密秘钥每次移动的位数是：0、1、2、2、2、2、2、2、1、2、2、2、2、2、2、1。

DES安全性分析

       
在相信复杂函数可以通过简单函数迭代若干圈得到的原则下，利用F函数及对合等运算，充分利用非线性运算。至今，最有效的破解DES算法的方法是穷举搜索法，那么56位长的密钥总共要测试256次，如果每100毫秒可以测试1次，那么需要7.2×1015秒，大约是228,493,000年。但是，仍有学者认为在可预见的将来用穷举法寻找正确密钥已趋于可行，所以若要安全保护10年以上的数据最好。现在多使用3DES加密。

加密&解密

import sys
# _pythonMajorVersion is used to handle Python2 and Python3 differences.
_pythonMajorVersion = sys.version_info[0]
# Modes of crypting / cyphering
ECB = 0
CBC = 1
# Modes of padding
PAD_NORMAL = 1
PAD_PKCS5 = 2


# PAD_PKCS5: is a method that will unambiguously remove all padding
#            characters after decryption, when originally encrypted with
#            this padding mode.
# For a good description of the PKCS5 padding technique, see:
# http://www.faqs.org/rfcs/rfc1423.html

# The base class shared by des and triple des.
class _baseDes(object):
    def __init__(self, mode=ECB, IV=None, pad=None, padmode=PAD_NORMAL):
        if IV:
            IV = self._guardAgainstUnicode(IV)
        if pad:
            pad = self._guardAgainstUnicode(pad)
        self.block_size = 8
        # Sanity checking of arguments.
        if pad and padmode == PAD_PKCS5:
            raise ValueError("Cannot use a pad character with PAD_PKCS5")
        if IV and len(IV) != self.block_size:
            raise ValueError("Invalid Initial Value (IV), must be a multiple of " + str(self.block_size) + " bytes")

        # Set the passed in variables
        self._mode = mode
        self._iv = IV
        self._padding = pad
        self._padmode = padmode

    def getKey(self):
        """getKey() -> bytes"""
        return self.__key

    def setKey(self, key):
        """Will set the crypting key for this object."""
        key = self._guardAgainstUnicode(key)
        self.__key = key

    def getMode(self):
        """getMode() -> pyDes.ECB or pyDes.CBC"""
        return self._mode

    def setMode(self, mode):
        """Sets the type of crypting mode, pyDes.ECB or pyDes.CBC"""
        self._mode = mode

    def getPadding(self):
        """getPadding() -> bytes of length 1. Padding character."""
        return self._padding

    def setPadding(self, pad):
        """setPadding() -> bytes of length 1. Padding character."""
        if pad is not None:
            pad = self._guardAgainstUnicode(pad)
        self._padding = pad

    def getPadMode(self):
        """getPadMode() -> pyDes.PAD_NORMAL or pyDes.PAD_PKCS5"""
        return self._padmode

    def setPadMode(self, mode):
        """Sets the type of padding mode, pyDes.PAD_NORMAL or pyDes.PAD_PKCS5"""
        self._padmode = mode

    def getIV(self):
        """getIV() -> bytes"""
        return self._iv

    def setIV(self, IV):
        """Will set the Initial Value, used in conjunction with CBC mode"""
        if not IV or len(IV) != self.block_size:
            raise ValueError("Invalid Initial Value (IV), must be a multiple of " + str(self.block_size) + " bytes")
        IV = self._guardAgainstUnicode(IV)
        self._iv = IV

    def _padData(self, data, pad, padmode):
        # Pad data depending on the mode
        if padmode is None:
            # Get the default padding mode.
            padmode = self.getPadMode()
        if pad and padmode == PAD_PKCS5:
            raise ValueError("Cannot use a pad character with PAD_PKCS5")

        if padmode == PAD_NORMAL:
            if len(data) % self.block_size == 0:
                # No padding required.
                return data

            if not pad:
                # Get the default padding.
                pad = self.getPadding()
            if not pad:
                raise ValueError("Data must be a multiple of " + str(
                    self.block_size) + " bytes in length. Use padmode=PAD_PKCS5 or set the pad character.")
            data += (self.block_size - (len(data) % self.block_size)) * pad

        elif padmode == PAD_PKCS5:
            pad_len = 8 - (len(data) % self.block_size)
            if _pythonMajorVersion < 3:
                data += pad_len * chr(pad_len)
            else:
                data += bytes([pad_len] * pad_len)

        return data

    def _unpadData(self, data, pad, padmode):
        # Unpad data depending on the mode.
        if not data:
            return data
        if pad and padmode == PAD_PKCS5:
            raise ValueError("Cannot use a pad character with PAD_PKCS5")
        if padmode is None:
            # Get the default padding mode.
            padmode = self.getPadMode()

        if padmode == PAD_NORMAL:
            if not pad:
                # Get the default padding.
                pad = self.getPadding()
            if pad:
                data = data[:-self.block_size] + \
                       data[-self.block_size:].rstrip(pad)

        elif padmode == PAD_PKCS5:
            if _pythonMajorVersion < 3:
                pad_len = ord(data[-1])
            else:
                pad_len = data[-1]
            data = data[:-pad_len]

        return data

    def _guardAgainstUnicode(self, data):
        # Only accept byte strings or ascii unicode values, otherwise
        # there is no way to correctly decode the data into bytes.
        if _pythonMajorVersion < 3:
            if isinstance(data, unicode):
                raise ValueError("pyDes can only work with bytes, not Unicode strings.")
        else:
            if isinstance(data, str):
                # Only accept ascii unicode values.
                try:
                    return data.encode('ascii')
                except UnicodeEncodeError:
                    pass
                raise ValueError("pyDes can only work with encoded strings, not Unicode.")
        return data
class des(_baseDes):
    """DES encryption/decrytpion class
    Supports ECB (Electronic Code Book) and CBC (Cypher Block Chaining) modes.
    pyDes.des(key,[mode], [IV])
    key  -> Bytes containing the encryption key, must be exactly 8 bytes
    mode -> Optional argument for encryption type, can be either pyDes.ECB
        (Electronic Code Book), pyDes.CBC (Cypher Block Chaining)
    IV   -> Optional Initial Value bytes, must be supplied if using CBC mode.
        Must be 8 bytes in length.
    pad  -> Optional argument, set the pad character (PAD_NORMAL) to use
        during all encrypt/decrypt operations done with this instance.
    padmode -> Optional argument, set the padding mode (PAD_NORMAL or
        PAD_PKCS5) to use during all encrypt/decrypt operations done
        with this instance.
    """

    # Permutation and translation tables for DES
    __pc1 = [56, 48, 40, 32, 24, 16, 8,
             0, 57, 49, 41, 33, 25, 17,
             9, 1, 58, 50, 42, 34, 26,
             18, 10, 2, 59, 51, 43, 35,
             62, 54, 46, 38, 30, 22, 14,
             6, 61, 53, 45, 37, 29, 21,
             13, 5, 60, 52, 44, 36, 28,
             20, 12, 4, 27, 19, 11, 3
             ]

    # number left rotations of pc1
    __left_rotations = [
        1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1
    ]

    # permuted choice key (table 2)
    __pc2 = [
        13, 16, 10, 23, 0, 4,
        2, 27, 14, 5, 20, 9,
        22, 18, 11, 3, 25, 7,
        15, 6, 26, 19, 12, 1,
        40, 51, 30, 36, 46, 54,
        29, 39, 50, 44, 32, 47,
        43, 48, 38, 55, 33, 52,
        45, 41, 49, 35, 28, 31
    ]

    # initial permutation IP
    __ip = [57, 49, 41, 33, 25, 17, 9, 1,
            59, 51, 43, 35, 27, 19, 11, 3,
            61, 53, 45, 37, 29, 21, 13, 5,
            63, 55, 47, 39, 31, 23, 15, 7,
            56, 48, 40, 32, 24, 16, 8, 0,
            58, 50, 42, 34, 26, 18, 10, 2,
            60, 52, 44, 36, 28, 20, 12, 4,
            62, 54, 46, 38, 30, 22, 14, 6
            ]

    # Expansion table for turning 32 bit blocks into 48 bits
    __expansion_table = [
        31, 0, 1, 2, 3, 4,
        3, 4, 5, 6, 7, 8,
        7, 8, 9, 10, 11, 12,
        11, 12, 13, 14, 15, 16,
        15, 16, 17, 18, 19, 20,
        19, 20, 21, 22, 23, 24,
        23, 24, 25, 26, 27, 28,
        27, 28, 29, 30, 31, 0
    ]

    # The (in)famous S-boxes
    __sbox = [
        # S1
        [14, 4, 13, 1, 2, 15, 11, 8, 3, 10, 6, 12, 5, 9, 0, 7,
         0, 15, 7, 4, 14, 2, 13, 1, 10, 6, 12, 11, 9, 5, 3, 8,
         4, 1, 14, 8, 13, 6, 2, 11, 15, 12, 9, 7, 3, 10, 5, 0,
         15, 12, 8, 2, 4, 9, 1, 7, 5, 11, 3, 14, 10, 0, 6, 13],

        # S2
        [15, 1, 8, 14, 6, 11, 3, 4, 9, 7, 2, 13, 12, 0, 5, 10,
         3, 13, 4, 7, 15, 2, 8, 14, 12, 0, 1, 10, 6, 9, 11, 5,
         0, 14, 7, 11, 10, 4, 13, 1, 5, 8, 12, 6, 9, 3, 2, 15,
         13, 8, 10, 1, 3, 15, 4, 2, 11, 6, 7, 12, 0, 5, 14, 9],

        # S3
        [10, 0, 9, 14, 6, 3, 15, 5, 1, 13, 12, 7, 11, 4, 2, 8,
         13, 7, 0, 9, 3, 4, 6, 10, 2, 8, 5, 14, 12, 11, 15, 1,
         13, 6, 4, 9, 8, 15, 3, 0, 11, 1, 2, 12, 5, 10, 14, 7,
         1, 10, 13, 0, 6, 9, 8, 7, 4, 15, 14, 3, 11, 5, 2, 12],

        # S4
        [7, 13, 14, 3, 0, 6, 9, 10, 1, 2, 8, 5, 11, 12, 4, 15,
         13, 8, 11, 5, 6, 15, 0, 3, 4, 7, 2, 12, 1, 10, 14, 9,
         10, 6, 9, 0, 12, 11, 7, 13, 15, 1, 3, 14, 5, 2, 8, 4,
         3, 15, 0, 6, 10, 1, 13, 8, 9, 4, 5, 11, 12, 7, 2, 14],

        # S5
        [2, 12, 4, 1, 7, 10, 11, 6, 8, 5, 3, 15, 13, 0, 14, 9,
         14, 11, 2, 12, 4, 7, 13, 1, 5, 0, 15, 10, 3, 9, 8, 6,
         4, 2, 1, 11, 10, 13, 7, 8, 15, 9, 12, 5, 6, 3, 0, 14,
         11, 8, 12, 7, 1, 14, 2, 13, 6, 15, 0, 9, 10, 4, 5, 3],

        # S6
        [12, 1, 10, 15, 9, 2, 6, 8, 0, 13, 3, 4, 14, 7, 5, 11,
         10, 15, 4, 2, 7, 12, 9, 5, 6, 1, 13, 14, 0, 11, 3, 8,
         9, 14, 15, 5, 2, 8, 12, 3, 7, 0, 4, 10, 1, 13, 11, 6,
         4, 3, 2, 12, 9, 5, 15, 10, 11, 14, 1, 7, 6, 0, 8, 13],

        # S7
        [4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1,
         13, 0, 11, 7, 4, 9, 1, 10, 14, 3, 5, 12, 2, 15, 8, 6,
         1, 4, 11, 13, 12, 3, 7, 14, 10, 15, 6, 8, 0, 5, 9, 2,
         6, 11, 13, 8, 1, 4, 10, 7, 9, 5, 0, 15, 14, 2, 3, 12],

        # S8
        [13, 2, 8, 4, 6, 15, 11, 1, 10, 9, 3, 14, 5, 0, 12, 7,
         1, 15, 13, 8, 10, 3, 7, 4, 12, 5, 6, 11, 0, 14, 9, 2,
         7, 11, 4, 1, 9, 12, 14, 2, 0, 6, 10, 13, 15, 3, 5, 8,
         2, 1, 14, 7, 4, 10, 8, 13, 15, 12, 9, 0, 3, 5, 6, 11],
    ]

    # 32-bit permutation function P used on the output of the S-boxes
    __p = [
        15, 6, 19, 20, 28, 11,
        27, 16, 0, 14, 22, 25,
        4, 17, 30, 9, 1, 7,
        23, 13, 31, 26, 2, 8,
        18, 12, 29, 5, 21, 10,
        3, 24
    ]

    # final permutation IP^-1
    __fp = [
        39, 7, 47, 15, 55, 23, 63, 31,
        38, 6, 46, 14, 54, 22, 62, 30,
        37, 5, 45, 13, 53, 21, 61, 29,
        36, 4, 44, 12, 52, 20, 60, 28,
        35, 3, 43, 11, 51, 19, 59, 27,
        34, 2, 42, 10, 50, 18, 58, 26,
        33, 1, 41, 9, 49, 17, 57, 25,
        32, 0, 40, 8, 48, 16, 56, 24
    ]

    # Type of crypting being done
    ENCRYPT = 0x00
    DECRYPT = 0x01

    # Initialisation
    def __init__(self, key, mode=ECB, IV=None, pad=None, padmode=PAD_NORMAL):
        # Sanity checking of arguments.
        if len(key) != 8:
            raise ValueError("Invalid DES key size. Key must be exactly 8 bytes long.")
        _baseDes.__init__(self, mode, IV, pad, padmode)
        self.key_size = 8

        self.L = []
        self.R = []
        self.Kn = [[0] * 48] * 16  # 16 48-bit keys (K1 - K16)
        self.final = []

        self.setKey(key)

    def setKey(self, key):
        """Will set the crypting key for this object. Must be 8 bytes."""
        _baseDes.setKey(self, key)
        self.__create_sub_keys()

    def __String_to_BitList(self, data):
        """Turn the string data, into a list of bits (1, 0)'s"""
        if _pythonMajorVersion < 3:
            # Turn the strings into integers. Python 3 uses a bytes
            # class, which already has this behaviour.
            data = [ord(c) for c in data]
        l = len(data) * 8
        result = [0] * l
        pos = 0
        for ch in data:
            i = 7
            while i >= 0:
                if ch & (1 << i) != 0:
                    result[pos] = 1
                else:
                    result[pos] = 0
                pos += 1
                i -= 1

        return result

    def __BitList_to_String(self, data):
        """Turn the list of bits -> data, into a string"""
        result = []
        pos = 0
        c = 0
        while pos < len(data):
            c += data[pos] << (7 - (pos % 8))
            if (pos % 8) == 7:
                result.append(c)
                c = 0
            pos += 1

        if _pythonMajorVersion < 3:
            return ''.join([chr(c) for c in result])
        else:
            return bytes(result)

    def __permutate(self, table, block):
        """Permutate this block with the specified table"""
        return list(map(lambda x: block[x], table))

    # Transform the secret key, so that it is ready for data processing
    # Create the 16 subkeys, K[1] - K[16]
    def __create_sub_keys(self):
        """Create the 16 subkeys K[1] to K[16] from the given key"""
        key = self.__permutate(des.__pc1, self.__String_to_BitList(self.getKey()))
        i = 0
        # Split into Left and Right sections
        self.L = key[:28]
        self.R = key[28:]
        while i < 16:
            j = 0
            # Perform circular left shifts
            while j < des.__left_rotations[i]:
                self.L.append(self.L[0])
                del self.L[0]

                self.R.append(self.R[0])
                del self.R[0]

                j += 1

            # Create one of the 16 subkeys through pc2 permutation
            self.Kn[i] = self.__permutate(des.__pc2, self.L + self.R)

            i += 1

    # Main part of the encryption algorithm, the number cruncher :)
    def __des_crypt(self, block, crypt_type):
        """Crypt the block of data through DES bit-manipulation"""
        block = self.__permutate(des.__ip, block)
        self.L = block[:32]
        self.R = block[32:]

        # Encryption starts from Kn[1] through to Kn[16]
        if crypt_type == des.ENCRYPT:
            iteration = 0
            iteration_adjustment = 1
        # Decryption starts from Kn[16] down to Kn[1]
        else:
            iteration = 15
            iteration_adjustment = -1

        i = 0
        while i < 16:
            # Make a copy of R[i-1], this will later become L[i]
            tempR = self.R[:]

            # Permutate R[i - 1] to start creating R[i]
            self.R = self.__permutate(des.__expansion_table, self.R)

            # Exclusive or R[i - 1] with K[i], create B[1] to B[8] whilst here
            self.R = list(map(lambda x, y: x ^ y, self.R, self.Kn[iteration]))
            B = [self.R[:6], self.R[6:12], self.R[12:18], self.R[18:24], self.R[24:30], self.R[30:36], self.R[36:42],
                 self.R[42:]]
            # Optimization: Replaced below commented code with above
            # j = 0
            # B = []
            # while j < len(self.R):
            #	self.R[j] = self.R[j] ^ self.Kn[iteration][j]
            #	j += 1
            #	if j % 6 == 0:
            #		B.append(self.R[j-6:j])

            # Permutate B[1] to B[8] using the S-Boxes
            j = 0
            Bn = [0] * 32
            pos = 0
            while j < 8:
                # Work out the offsets
                m = (B[j][0] << 1) + B[j][5]
                n = (B[j][1] << 3) + (B[j][2] << 2) + (B[j][3] << 1) + B[j][4]

                # Find the permutation value
                v = des.__sbox[j][(m << 4) + n]

                # Turn value into bits, add it to result: Bn
                Bn[pos] = (v & 8) >> 3
                Bn[pos + 1] = (v & 4) >> 2
                Bn[pos + 2] = (v & 2) >> 1
                Bn[pos + 3] = v & 1

                pos += 4
                j += 1

            # Permutate the concatination of B[1] to B[8] (Bn)
            self.R = self.__permutate(des.__p, Bn)

            # Xor with L[i - 1]
            self.R = list(map(lambda x, y: x ^ y, self.R, self.L))
            # Optimization: This now replaces the below commented code
            # j = 0
            # while j < len(self.R):
            #	self.R[j] = self.R[j] ^ self.L[j]
            #	j += 1

            # L[i] becomes R[i - 1]
            self.L = tempR

            i += 1
            iteration += iteration_adjustment

        # Final permutation of R[16]L[16]
        self.final = self.__permutate(des.__fp, self.R + self.L)
        return self.final

    # Data to be encrypted/decrypted
    def crypt(self, data, crypt_type):
        """Crypt the data in blocks, running it through des_crypt()"""

        # Error check the data
        if not data:
            return ''
        if len(data) % self.block_size != 0:
            if crypt_type == des.DECRYPT:  # Decryption must work on 8 byte blocks
                raise ValueError(
                    "Invalid data length, data must be a multiple of " + str(self.block_size) + " bytes\n.")
            if not self.getPadding():
                raise ValueError("Invalid data length, data must be a multiple of " + str(
                    self.block_size) + " bytes\n. Try setting the optional padding character")
            else:
                data += (self.block_size - (len(data) % self.block_size)) * self.getPadding()
        # print "Len of data: %f" % (len(data) / self.block_size)

        if self.getMode() == CBC:
            if self.getIV():
                iv = self.__String_to_BitList(self.getIV())
            else:
                raise ValueError("For CBC mode, you must supply the Initial Value (IV) for ciphering")

        # Split the data into blocks, crypting each one seperately
        i = 0
        dict = {}
        result = []
        # cached = 0
        # lines = 0
        while i < len(data):
            # Test code for caching encryption results
            # lines += 1
            # if dict.has_key(data[i:i+8]):
            # print "Cached result for: %s" % data[i:i+8]
            #	cached += 1
            #	result.append(dict[data[i:i+8]])
            #	i += 8
            #	continue

            block = self.__String_to_BitList(data[i:i + 8])

            # Xor with IV if using CBC mode
            if self.getMode() == CBC:
                if crypt_type == des.ENCRYPT:
                    block = list(map(lambda x, y: x ^ y, block, iv))
                # j = 0
                # while j < len(block):
                #	block[j] = block[j] ^ iv[j]
                #	j += 1

                processed_block = self.__des_crypt(block, crypt_type)

                if crypt_type == des.DECRYPT:
                    processed_block = list(map(lambda x, y: x ^ y, processed_block, iv))
                    # j = 0
                    # while j < len(processed_block):
                    #	processed_block[j] = processed_block[j] ^ iv[j]
                    #	j += 1
                    iv = block
                else:
                    iv = processed_block
            else:
                processed_block = self.__des_crypt(block, crypt_type)

            # Add the resulting crypted block to our list
            # d = self.__BitList_to_String(processed_block)
            # result.append(d)
            result.append(self.__BitList_to_String(processed_block))
            # dict[data[i:i+8]] = d
            i += 8

        # print "Lines: %d, cached: %d" % (lines, cached)

        # Return the full crypted string
        if _pythonMajorVersion < 3:
            return ''.join(result)#
        else:
            return bytes.fromhex('').join(result)

    def encrypt(self, data, pad=None, padmode=None):
        """encrypt(data, [pad], [padmode]) -> bytes
        data : Bytes to be encrypted
        pad  : Optional argument for encryption padding. Must only be one byte
        padmode : Optional argument for overriding the padding mode.
        The data must be a multiple of 8 bytes and will be encrypted
        with the already specified key. Data does not have to be a
        multiple of 8 bytes if the padding character is supplied, or
        the padmode is set to PAD_PKCS5, as bytes will then added to
        ensure the be padded data is a multiple of 8 bytes.
        """
        data = self._guardAgainstUnicode(data)
        if pad is not None:
            pad = self._guardAgainstUnicode(pad)
        data = self._padData(data, pad, padmode)
        return self.crypt(data, des.ENCRYPT)

    def decrypt(self, data, pad=None, padmode=None):
        """decrypt(data, [pad], [padmode]) -> bytes
        data : Bytes to be decrypted
        pad  : Optional argument for decryption padding. Must only be one byte
        padmode : Optional argument for overriding the padding mode.
        The data must be a multiple of 8 bytes and will be decrypted
        with the already specified key. In PAD_NORMAL mode, if the
        optional padding character is supplied, then the un-encrypted
        data will have the padding characters removed from the end of
        the bytes. This pad removal only occurs on the last 8 bytes of
        the data (last data block). In PAD_PKCS5 mode, the special
        padding end markers will be removed from the data after decrypting.
        """
        data = self._guardAgainstUnicode(data)
        if pad is not None:
            pad = self._guardAgainstUnicode(pad)
        data = self.crypt(data, des.DECRYPT)
        return self._unpadData(data, pad, padmode)

#from pyDes import *
# For python2，
#   data = "Please encrypt my data"
#   k = des("DESCRYPT", CBC, "\0\0\0\0\0\0\0\0", pad=None, padmode=PAD_PKCS5)
# For Python3, you'll need to use bytes, i.e.:
"""data = b"Please encrypt my data"
k = des(b"DESCRYPT", CBC, b"\0\0\0\0\0\0\0\0", pad=None, padmode=PAD_PKCS5)
d = k.encrypt(data)
print("Encrypted: %r" % d)
print("Decrypted: %r" % k.decrypt(d))
assert k.decrypt(d, padmode=PAD_PKCS5) == data"""
from time import  time
print ("Example of DES encryption using CBC mode\n")
t = time()
k = des("KANBEKTR",CBC, "\0\0\0\0\0\0\0\0",pad=None, padmode=PAD_PKCS5)
data = "CUMT-BXS"
print ("Key    : %r" % k.getKey())
print ("Data   : %r" % data)
d = k.encrypt(data)
print ("Encrypt: %r" % d)
d = k.decrypt(d)
print ("Decrypt: %r" % d)
#print ("DES time taken: %f (6 crypt operations)" % (time() - t))
print ("")

程序运行截图

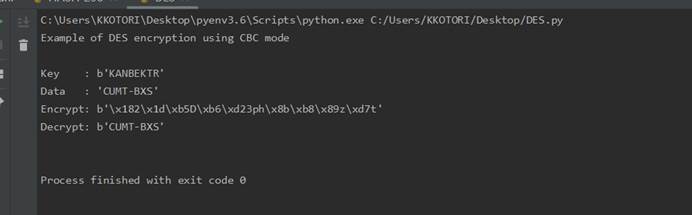
序列密码

线性移位寄存器（LFSR）

线性反馈移位寄存器（linear feedback shift register， LFSR）是指，给定前一状态的输出，将该输出的线性函数再用作输入的移位寄存器。异或运算是最常见的单比特线性函数：对寄存器的某些位进行异或操作后作为输入，再对寄存器中的各比特进行整体移位。
线性反馈移位寄存器（LFSR）是一个产生二进制位序列的机制。这个寄存器由一个初始化矢量设置的一系列信元组成，最常见的是，密钥。这个寄存器的行为被一个时钟调节。在每个定时时刻，这个寄存器信元的内容被移动到一个正确的位置，这个排外的或这个信元子集内的内容被放在最左边的信元中。输出的一个位通常来自整个更新程序。LFSRs的应用包括产生伪随机数字，伪噪声序列，快速数字计算器和灰数序列。LFSR软件和硬件的执行是相同的。

实现

#include <iostream>
#include <string>
#include <string.h>
using namespace std;
char rg[100];
char jrg[100];
int sc[100];
char fs[100];
char res[1000000];
int main(){
	memset(rg,'\0',sizeof(rg));//100000000000001 
	memset(fs,'\0',sizeof(fs));//100000000000001 
	//memset(jrg,'\0',sizeof(jrg));
	scanf("%s",&rg);
	scanf("%s",&fs);
	int l=0;
	for(int i=0;i<strlen(fs);i++){
		if(fs[i] == '1'){
			sc[l]=strlen(fs)-i;
			cout<<sc[l]<<endl;
			l++;
		}
		cout<<l<<" "<<strlen(fs)<<" "<<strlen(rg)<<endl;
	}
	int t,c,time;
	//scanf("%d",&t);
	strcpy(jrg,rg);
	//printf("%s\n",jrg);
	for(int i=0;;i++){
		c=rg[sc[l-1]-1];
		for(int j=l-2;j>=0;j--){
			//res[i]=fs[j-1]^fs[j];
			c=char(((int(c))+int(rg[sc[j]-1]))%2+'0');
		}	//xor
		res[i]=rg[strlen(rg)-1];
		for(int k=strlen(rg)-1;k>0;k--){
			rg[k]=rg[k-1];
		}	//>>1
		rg[0]=c;
		printf("%s\n",rg);
		if(!strcmp(rg,jrg)){
			break;
		}
		time=i+2;
	}
	printf("周期为:%d\n",time);
	printf("%s\n",res);
	
}

程序运行截图

 

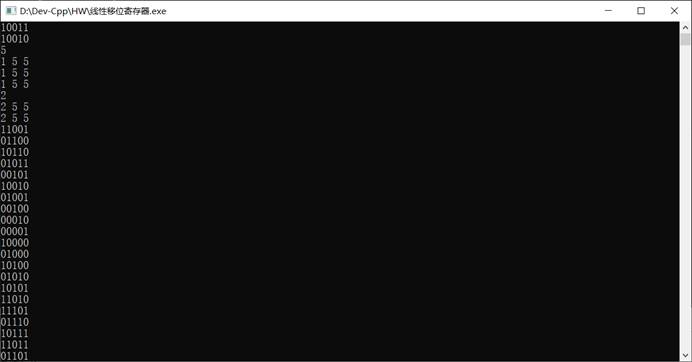
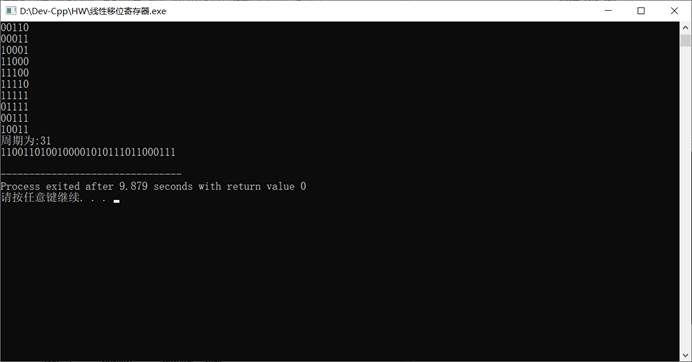
哈希函数

SHA-256分析

初始化

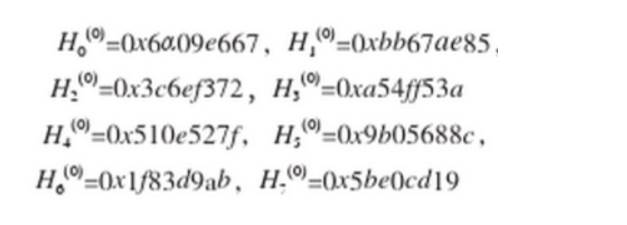
准备消息列表

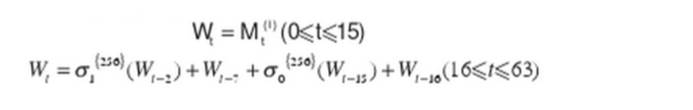
轮散列值初始化

用每一轮的散列值的中间结果初始化8个工作变量A、B、C、D、E、F、G、H。初始定义由H0(0)-H7(7)给出。

压缩函数

对于0≤t≤63,执行（即压缩函数）：
T1=H+∑1{256}(e)+Ch(e,f,g)+Kt{256}+Wt
T2=∑0{256}(a)+Maj(a,b,c)
H=g g=h e=d+T1 d=c
c=b b=a a=T1+T2

每组的中间散列值计算方法

H₀⁽ⁱ⁾=a+H₀^(i-j),
H₁⁽ⁱ⁾=b+H₁^(i-j), H₂⁽ⁱ⁾=c+H₂^(i-j),
H₃⁽ⁱ⁾=d+H₃^(i-j), H₄⁽ⁱ⁾=e+H₄^(i-j),
H₅⁽ⁱ⁾=f+H₅^(i-j), H₆⁽ⁱ⁾=g+H₆^(i-j),
H₇⁽ⁱ⁾=h+H₇^(i-j)

这里i是指消息的第i个分组，将所有的分组处理完毕后，最后输出256比特的Hash值：
H₀^(N) | | H₁^(N)
| | H₂^(N) | | H₃^(N) | | H₄^(N)
| | H₅^(N) H₆^(N) | | H₇^(N)

算法中使用的6个逻辑函数：

SHA-256安全分析

Hash函数的安全性很大程度上取决于抗强碰撞的能力，即攻击者找出两个涓息M和M^tM≠M^t，使得H(M)=HM^t  ,因此，评价一个Hash函数的安全性，就是看攻击者在现有的条件下，是否可以找到该函数的一对碰撞。目前已有的对Hash函数攻击的方法包括生日攻击、彩虹表攻击、差分攻击等。

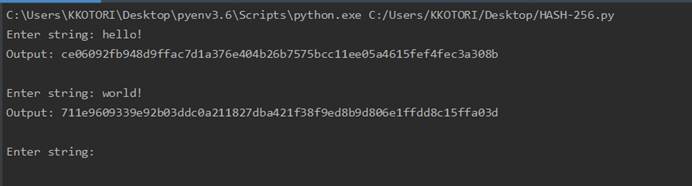
实现

class SHA256:
    def __init__(self):

        self.W = 32
        self.M = 1 << self.W
        self.FF = self.M - 1

        self.constants = (
            0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5,
            0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
            0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
            0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
            0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc,
            0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
            0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
            0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
            0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
            0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
            0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3,
            0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
            0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5,
            0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
            0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
            0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2)

        self.compression_vals = (
            0x6a09e667, 0xbb67ae85, 0x3c6ef372, 0xa54ff53a,
            0x510e527f, 0x9b05688c, 0x1f83d9ab, 0x5be0cd19)

    def ShiftRight(self, x, b):
        return ((x >> b) | (x << (self.W - b))) & self.FF

    def Pad(self, W):
        return bytes(W, "ascii") + b"\x80" + (b"\x00" * ((55 if (len(W) % 64) < 56 else 119) - (len(W) % 64))) + (
            (len(W) << 3).to_bytes(8, "big"))

    def Compress(self, Wt, Kt, A, B, C, D, E, F, G, H):
        return ((H + (self.ShiftRight(E, 6) ^ self.ShiftRight(E, 11) ^ self.ShiftRight(E, 25)) + (
                    (E & F) ^ (~E & G)) + Wt + Kt) + (
                            self.ShiftRight(A, 2) ^ self.ShiftRight(A, 13) ^ self.ShiftRight(A, 22)) + (
                            (A & B) ^ (A & C) ^ (B & C))) & self.FF, A, B, C, (D + (
                    H + (self.ShiftRight(E, 6) ^ self.ShiftRight(E, 11) ^ self.ShiftRight(E, 25)) + (
                        (E & F) ^ (~E & G)) + Wt + Kt)) & self.FF, E, F, G

    def hash(self, message):
        message = self.Pad(message)
        digest = list(self.compression_vals)

        for i in range(0, len(message), 64):
            S = message[i: i + 64]
            W = [int.from_bytes(S[e: e + 4], "big") for e in range(0, 64, 4)] + ([0] * 48)

            for j in range(16, 64):
                W[j] = (W[j - 16] + (
                            self.ShiftRight(W[j - 15], 7) ^ self.ShiftRight(W[j - 15], 18) ^ (W[j - 15] >> 3)) + W[
                            j - 7] + (self.ShiftRight(W[j - 2], 17) ^ self.ShiftRight(W[j - 2], 19) ^ (
                            W[j - 2] >> 10))) & self.FF

            A, B, C, D, E, F, G, H = digest

            for j in range(64):
                A, B, C, D, E, F, G, H = self.Compress(W[j], self.constants[j], A, B, C, D, E, F, G, H)

        return "".join(format(h, "02x") for h in b"".join(
            d.to_bytes(4, "big") for d in [(x + y) & self.FF for x, y in zip(digest, (A, B, C, D, E, F, G, H))]))


def main():
    encoder = SHA256()

    while True:
        message = input("Enter string: ")
        print(f"Output: {encoder.hash(message)}\n")


if __name__ == "__main__":
    main()

程序运行截图

RSA

基于RSA的数字签名

用RSA进行数字签名

在RSA中，被签名的消息，密钥以及最终生成的签名都是以数字形式表示的，需要实现对文本编码成数字。用RSA生成签名的过程可以用下面的公式来表达。

 

               
这里使用的D和N就是签名者的私钥。签名就是对消息的D次方求mod N的结果，也就是说将消息和自己相乘D次，然后再求N的模数，最后求得的数就是签名。

用RSA验证签名

                
RSA的签名验证过程可用下列公式来表达：

这里所使用的E和N就是签名者的公钥。接收者计算签名的E次方并求mod N，得到“由签名求得的消息”，并将其发送过来的签名内容进行对比，如果两者一致，则签名验证成功，否则签名验证失败。

RSA签名生成和验证过程如图：

A，B之间进行签名

1.首先，A对明文M进行哈希加密，得到H（M），然后将H（M）^d mod N 求出签名值S；

2.A将M和s一齐发送给<spanlang=EN-US>B；

3.B收到消息后，首先将明文M进行哈希加密。然后判断H（M）=s^e(mod n)是否成立。如果成立则签名成功。

注：d，e，n都是rsa加密算法中的参数。

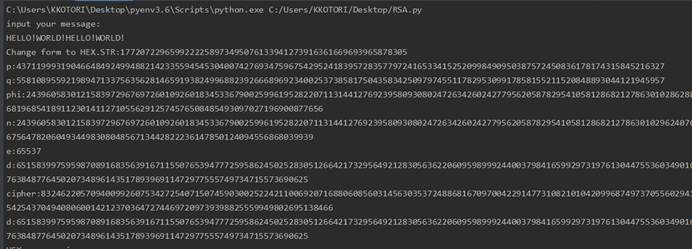
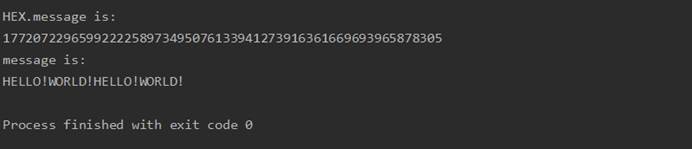
实现

import binascii
import math
import random

def gcd(a, b):  #欧几里得除法
    if a > b: a, b = b, a   #a先被赋值b的地址于是b再被赋值a的地址
    while b != 0:
        a, b = b, a%b
    return a

def isPrime(n):     #平凡除法
    if n <= 1:
        return False
    for i in range(2, int(math.sqrt(n)) + 1):
        if n % i== 0:
            return False
    return True

def prime_test(n):  #素性检验   Miller-Rabin
    q = n - 1
    k = 0           # 寻找k,q 是否满足2^k*q =n - 1
    while q % 2 == 0:
        k += 1
        q = q // 2
    a = random.randint(2, n - 2)    # 如果 a^q mod n= 1, n 可能是一个素数
    if fast_pow(a, q, n) == 1:
        return True     # 如果存在j满足 a ^ ((2 ^ j) * q) mod n == n-1, n 可能是一个素数
    for j in range(0, k):
        if fast_pow(a, (2 ** j) * q, n) == n - 1:
            return True     # n 不是素数
    return False

def fast_pow(b, n, m):  #快速幂
    ret = 1
    tmp = b
    while n:
        if n & 0x1:
            ret = ret * tmp % m
        tmp = tmp * tmp % m
        n >>= 1
    return ret

def ext_gcd(a, b):      #s*a+t*b=1
    if b == 0:
        return 1, 0, a
    else:
        x, y, q = ext_gcd(b, a % b)
        x, y = y, (x - (a // b) * y)
        return x, y, q

def generate_d(phi, e):
    (x, y, r) = ext_gcd(phi, e)    # y maybe < 0, so convert it
    if y < 0:   #return y % ph_n
        return y + phi     #直接用加法效率高一丢丢
    return y

def generate_key(key_len):  #key_len要比消息长度大的多
    p = random_prime(key_len // 2)
    q = random_prime(key_len // 2)
    print("p:"+str(p))
    print("q:"+str(q))
    n = p * q
    phi = (p -1) * (q -1)
    print("phi:"+str(phi))
    e = 65537 #e取固定值
    d = generate_d(phi, e)
    return (n ,e, d)

def random_prime(half_len):     #随机产生p、q
    while True:
        n = random.randint(0, 1 << half_len)    #求2^half_len之间的大数
        if n % 2 != 0:
            found = True        # 随机性测试
            for i in range(0, 5):       #5的时候错误率已经小于千分之一
                if prime_test(n) == False:
                    found = False
                    break
            if found == True:
                return n

def mess2long(message):         #字符串转HEX
	return int(message.encode().hex(),16)

def long2mess(long_num):        #解密，HEX转字符串
    long_mess = hex(long_num)[2:].replace("L","")
    if len(long_mess) % 2 != 0: long_mess = '0' + long_mess
    return long_mess    #binascii.unhexlify(long2mess(plain_num)).decode()

message =input("input your message:\n")
mess_num = mess2long(message)
print("Change form to HEX.STR:"+str(mess_num))
mess_num_length = len(str(mess_num))
(n, e, d) = generate_key(mess_num_length*15)
print("n:"+str(n))
print("e:"+str(e))
print("d:"+str(d))
cipher = fast_pow(mess_num,e, n)
print("cipher:"+str(cipher))
print("d:"+str(d))
plain_num = fast_pow(cipher, d, n)
print("HEX.message is:")
print(str(int(long2mess(plain_num),16)))
print("message is:")
print(binascii.unhexlify(long2mess(plain_num)).decode())

程序运行截图

综合实验

Alice想通过公共信道给Bob传输一份秘密文件（文件非常大），又知道，很多人和机构想得到这份文件。如果你是Alice，你应该怎样做？请设计一个方案，并编程实现。

程序没编，但是思路想好了。

具体思路：

1.首先，A要发送的明文为M，A选择DES加密，则先对明文进行DES加密，则加密后的密文为C。

2.为了防止有人伪造A对B发送消息，则A对密文C进行基于RSA的数字签名。首先确定RSA的私钥d，公钥e，n；

3.首先A对密文进行哈希函数得到H(C),然后通过RSA的私钥D进行消息的“解密”，即Si=H(Ci)^d(mod n),随后 A将C与S发送给B。

4.B收到A发送过来的（C,S）之后，进行消息的验证。首先B先计算C对应的哈希值，并且与Si^e（mod n）比较是否同余，如果相同，则说明B收到的就是来自A发送的消息，发送过程中没有人进行消息的篡改和伪造。

5.B然后应用DES的解密算法和密钥进行解密，则得到明文M。